Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Трехмерное евклидово пространство / 1 2 3 4 5 6 7 8 9 10 11 12 13
10. Кватернионы. Как и коммутирование, умножение операторов из
так что
или, как пишут физики,
Отсюда видно, что вещественное пространство операторов
с таблицей умножения i2 = j2 = k2 = - 1, ij = - ji = k, ki = - ik = j; jk = - kj = i. Другими словами, получаем тело кватернионов в одном из традиционных матричных представлений. -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
 , вообще говоря, выводит нас за пределы
, вообще говоря, выводит нас за пределы 

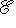 , причем "вещественная часть" есть как раз скалярное произведение, а "мнимая" - векторное. Действительно,
, причем "вещественная часть" есть как раз скалярное произведение, а "мнимая" - векторное. Действительно,

 при
при