Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Жорданова нормальная форма / 1 2 3 4 5 6 7 8 9 10
Каждый столбец, таким образом, изображает базис инвариантного подпространства, отвечающего одной жордановой клетке, размер которой равен высоте этого столбца (числу точек в нем): если
то
Наоборот, если мы найдем в L базис, элементы которого f переводит в другие его элементы или в нуль так, что элементы этого базиса вместе с действием f можно изобразить подобной диаграммой, то он будет жордановым базисом для L. Проведем доказательство существования индукцией по размерности L. Если dim L = 1, то нильпотентный оператор f является нулевым, и любой ненулевой вектор в L образует его жорданов базис. Пусть теперь dim L = n > 1, и пусть для размерностей, меньших n, существование жорданова базиса уже доказано. Обозначим через По индуктивному предположению |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
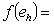
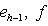
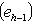
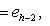
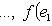
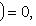
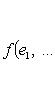
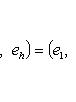
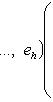



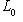
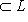 подпространство собственных векторов для f, т. е. Ker f. Так как dim L0 > 0, имеем dim L/L0 < n, а оператор
подпространство собственных векторов для f, т. е. Ker f. Так как dim L0 > 0, имеем dim L/L0 < n, а оператор 
 индуцирует оператор
индуцирует оператор 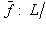
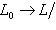
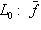
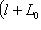
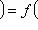
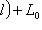 .
. имеет жорданов базис. Можем считать его непустым: иначе L = L0, и любой базис L0 будет жордановым для
имеет жорданов базис. Можем считать его непустым: иначе L = L0, и любой базис L0 будет жордановым для