Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Жорданова нормальная форма / 1 2 3 4 5 6 7 8 9 10
так что
Из последнего же соотношения следует, что все ai = 0, потому что векторы Наконец, покажем, что если имеется любая нетривиальная линейная комбинация векторов D, равная нулю, то из нее можно получить нетривиальную линейную зависимость между векторами нижней строки D. В самом деле, отметим самую верхнюю строку D, в которой имеются ненулевые коэффициенты этой воображаемой линейной комбинации. Пусть номер этой строки (считая снизу) равен h. Применим к этой комбинации оператор fh-1. Очевидно, ее часть, отвечающая h-й строке, перейдет в нетривиальную линейную комбинацию элементов нижней строки, а остальные слагаемые обратятся в нуль. Это завершает доказательство предположения. Теперь осталось проверить часть теоремы из п. 1, относящуюся к единственности. 8. Пусть фиксирован произвольный жорданов базис оператора f. Любой диагональный элемент матрицы оператора f в этом базисе, очевидно, является одним из собственных значений |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
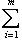
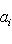
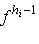
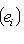
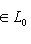 и
и 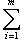
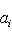
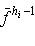
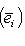
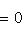 .
.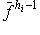
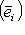 составляют нижнюю строку диаграммы
составляют нижнюю строку диаграммы  и являются частью базиса L/L0.
и являются частью базиса L/L0. этого оператора. Рассмотрим часть базиса, отвечающего всем блокам матрицы с этим значением
этого оператора. Рассмотрим часть базиса, отвечающего всем блокам матрицы с этим значением 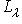 его линейную оболочку. Поскольку
его линейную оболочку. Поскольку 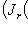
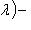
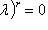 , имеем
, имеем 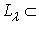
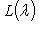 , где
, где 
 - корневое подпространство L. Кроме того,
- корневое подпространство L. Кроме того, 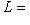
 по определению жорданова базиса и
по определению жорданова базиса и 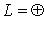
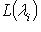 по предложению п. 5, где в обоих случаях
по предложению п. 5, где в обоих случаях 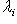 пробегает все собственные значения оператора f по одному разу. Следовательно,
пробегает все собственные значения оператора f по одному разу. Следовательно, 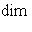
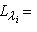

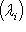 и
и 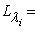
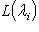 . Значит, сумма размеров жордановых клеток, отвечающих каждому
. Значит, сумма размеров жордановых клеток, отвечающих каждому 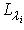 . Поэтому достаточно проверить теорему единственности для случая
. Поэтому достаточно проверить теорему единственности для случая 
 или даже для L = L(0).
или даже для L = L(0).