6. Предложение. Расстояние от l до L₀ равно длине ортогональной проекции l на .

Доказательство. Для любого вектора имеем

в силу теоремы Пифагора, т. к. векторы и ортогональны. Следовательно,

и равенство достигается только в случае m = l₀, что доказывает требуемое.

Если в L₀ выбран ортонормированный базис {e₁, ..., e_m}, то проекция l на L₀ определяется формулой

Действительно, левая и правая части имеют одинаковые скалярные произведения со всеми e_i, поэтому их разность лежит в . Окончательно,

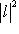есть наименьшее значение | l - m |, когда m пробегает L₀. Поскольку по той же теореме Пифагора, имеем

-1-2-3-4-5-6-7-8-9-10-11-12-13-14-