Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Геометрия квадратичных форм и собственные значения самосопряженных операторов / 1 2 3 4 5 6 7 8 9 10 11
10. Теорема. Для любого подпространства
Эти оценки точны для некоторых L' (например,
Доказательство. Поскольку
а |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
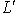
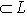 коразмерности k - 1 справедливы неравенства:
коразмерности k - 1 справедливы неравенства: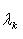
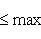
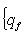
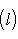
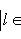
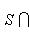
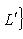
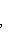
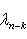
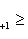
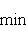
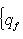
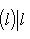
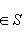
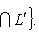
 и
и  соответственно), так что
соответственно), так что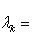
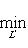
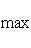
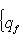
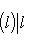
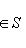
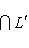
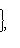
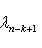
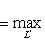
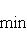
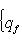
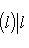
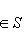
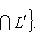
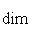
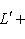
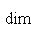
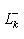
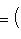
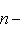
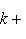
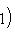
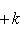
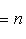
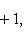
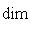
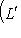
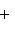
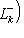
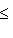
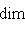
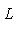
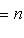 , из теоремы
, из теоремы 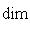
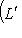
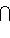
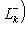
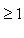 . Возьмем вектор
. Возьмем вектор 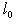
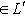
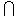
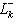
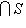 . Согласно следствию 9
. Согласно следствию 9 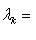
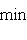
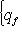
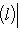
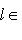
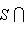
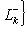 , так что
, так что 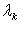
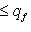
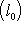 и тем более
и тем более 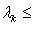
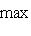
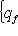
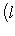
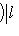
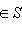
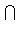
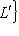 . Второе неравенство теоремы проще всего получить, применив первое неравенство к оператору - f и заметив, что знаки и порядок собственных значений при этом обращаются.
. Второе неравенство теоремы проще всего получить, применив первое неравенство к оператору - f и заметив, что знаки и порядок собственных значений при этом обращаются.