Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Линейные отображения / 1 2 3 4 5 6 7 8 9
Его линейность проверяется непосредственно. В этом доказательстве использовалась разность двух линейных отображений 4. Обозначим через (af)(l) = a(f(l)), (f + g)(l) = f(l) + g(l) для всех 5. Пусть (gf)(l1 + l2) = g[f(l1 + l2)] = g[f(l1) + f(l2)] = g[f(l1)] + g[f(l2)] = gf(l1) + gf(l2) и, аналогично, (gf)(al) = a(gf(l)). Очевидно, idM |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

 . Это частный случай следующей более общей конструкции.
. Это частный случай следующей более общей конструкции.
 множество линейных отображений из L в M. Для
множество линейных отображений из L в M. Для 

 и
и 
 определим af и f + g формулами
определим af и f + g формулами
 . Проверяется (по аналогии как делали
. Проверяется (по аналогии как делали 

 и
и 

 . Теоретико-множественная композиция
. Теоретико-множественная композиция 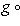



 является линейным отображением. Действительно,
является линейным отображением. Действительно, f = f
f = f