Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Геометрия пространств со скалярным произведением / Пространство Минковского / 1 2 3 4 5 6 7 8 9 10 11 12 13
т. е. x = (l1, l2) -1. Расстояние от l1 до xl2 пространственноподобно: для наблюдателя Rl1 - это расстояние, на которое Rl2 удалился от него за единицу времени, т. е. относительная скорость Rl2. Она равна (учесть, что у метрики в v = [ - (xl2 - l1, xl2 - l1)]1/2 = [ - (xl2 - l1, xl2)]1/2 = = [ - x2(l2, l2) + x(l1, l2)]1/2 = [ -(l1, l2) -2 + 1]1/2, откуда
Это знаменитый множитель Лоренца; часто его пишут в виде
т. е. в момент собственного времени единица для первого наблюдателя второй наблюдатель находится в его физическом пространстве, когда часы второго наблюдателя показывают 9. Евклидовы углы. В пространстве -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
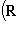
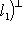 следует изменить знак!)
следует изменить знак!)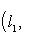
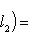
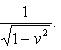
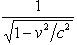 , явно указывая, что скорости измеряются по отношению к скорости света. В частности,
, явно указывая, что скорости измеряются по отношению к скорости света. В частности,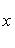
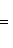
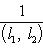

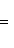
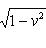
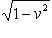 . Это - количественное выражение эффекта "сокращения времени" для движущегося наблюдателя, качественно описанное в предыдущем пункте.
. Это - количественное выражение эффекта "сокращения времени" для движущегося наблюдателя, качественно описанное в предыдущем пункте.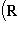
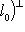 , где l0 - времениподобный вектор, геометрия евклидова, и там скалярное произведение имеет обычный смысл. Пусть l1, l2 - еще два времениподобных вектора с той же ориентацией. Мы можем спроектировать их на
, где l0 - времениподобный вектор, геометрия евклидова, и там скалярное произведение имеет обычный смысл. Пусть l1, l2 - еще два времениподобных вектора с той же ориентацией. Мы можем спроектировать их на 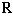
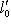 увидит его другим.
увидит его другим.