Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Базис и размерность / 1 2 3 4 5 6 7 8 9 10 11
Положим
Поскольку {ei} образуют базис в L, нулевой вектор имеет единственное представление
Поскольку число неизвестных m больше числа уравнений n, эта система имеет ненулевое решение. Теорема доказана. 5. Замечания. а) Можно было бы рассматривать произвольные семейства векторов и называть такое семейство базисом, если любой вектор пространства однозначно представляется в виде конечной линейной комбинации элементов семейства. В этом смысле любое линейное пространство имеет базис, и у бесконечномерного пространства базис всегда бесконечен. Однако это понятие не слишком полезно. Как правило, бесконечномерные пространства снабжаются топологией, и определение базиса видоизменяется с учетом этой топологии и возможности определять некоторые бесконечные линейные комбинации. б) В общих линейных пространствах базисные векторы по традиции нумеруются целыми числами от 1 до n (иногда от 0 до n), но это совершенно не обязательно. Базис |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
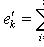


 . Для любых
. Для любых 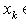
 имеем
имеем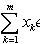



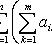
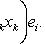

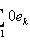 в виде линейной комбинации {ek}. Поэтому условие
в виде линейной комбинации {ek}. Поэтому условие 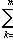
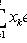
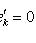 равносильно системе однородных линейных уравнений относительно xk:
равносильно системе однородных линейных уравнений относительно xk: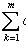

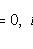
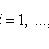

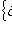
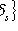 в F(S) естественно нумеруется элементами множества
в F(S) естественно нумеруется элементами множества 
 . Можно также считать базис L просто подмножеством в L, элементы которого не снабжены никакими индексами. Нумерация, или, скорее, порядок элементов базиса, существенны при использовании матричного формализма. В других вопросах может оказаться важной другая структура на множестве индексов базиса. Например, если S - конечная группа, то важно, как индексы s базиса
. Можно также считать базис L просто подмножеством в L, элементы которого не снабжены никакими индексами. Нумерация, или, скорее, порядок элементов базиса, существенны при использовании матричного формализма. В других вопросах может оказаться важной другая структура на множестве индексов базиса. Например, если S - конечная группа, то важно, как индексы s базиса