Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
Артелак всплеск 10мл флак цена артелак капли для глаз цена Glavlinza. ; https://gk-rushim.ru ортофосфорная кислота купить в нижнем. Фосфорная кислота купить.
|
Геометрия пространств со скалярным произведением / Теоремы классификации / 1 2 3 4 5 6 7 8 9 10 11 12 13
Это противоречие завершает доказательство того, что у изометричных пространств сигнатуры, вычисленные по любым ортогональным разложениям, одинаковы. Наоборот, если (L, g), (L', g') - два пространства с одинаковыми сигнатурами, то между подпространствами из их ортогональных разложений Теперь выведем несколько следствий и переформулировок теорем пп. 3 и 5, которые подчеркивают разные аспекты ситуации. 6. Базисы. Пусть (L, g) - пространство со скалярным произведением. Базис {e1, ..., en} в L называется ортогональным, если g(ei, ej) = 0 для всех Ортогональный базис {ei} называется ортонормированным, если g(ei, ei) = 0 или -1-2-3-4-5-6-7-8-9-10-11-12-13- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник

 и
и 
 можно установить взаимно однозначное соответствие
можно установить взаимно однозначное соответствие 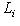
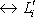 , сохраняющее знак ограничения g на Li и g' на
, сохраняющее знак ограничения g на Li и g' на 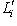 соответственно. По результатам
соответственно. По результатам 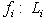
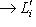 , и их прямая сумма
, и их прямая сумма 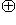
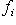 будет изометрией между L и L'.
будет изометрией между L и L'.
 для всех i. Обсуждение в конце раздела
для всех i. Обсуждение в конце раздела