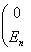Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Комплексификация и овеществление / 1 2 3 4 5 6 7 8 9 10 11
Доказательство. Обе аксиомы дистрибутивности легко проверяются, исходя из линейности J и формул сложения комплексных чисел. Проверим аксиому ассоциативности умножения: (a + bi)[(c + di)l] = (a + bi)[cl + dJ(l)] = a[cl + dJ(l)] + + bJ[cl + dJ(l)] = acl + adJ(l) + bcJ(l) - bdl = (ac - db)l + + (ad + bc)J(l) = [ac - bd + (ad + bc)i]l = [(a + bi)(c + di)]l. Все остальные аксиомы выполнены по той причине, что L и 8. Следствие. Если (L, J) - конечномерное вещественное пространство с комплексной структурой, то dimR L = 2n четна, и матрица J в подходящем базисе имеет вид
Доказательство. Действительно, dimR L = 2 dimC |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
 совпадают как аддитивные группы.
совпадают как аддитивные группы.