Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Матрицы / 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Кроме того, произведение матриц линейно по каждому аргументу: (aA + bB)C = aAC + bBC; A(bB + cC) = aAB + cAC. Важнейшее свойство умножения матриц состоит в том, что оно отвечает композиции линейных отображений. Однако целый ряд других ситуаций в линейной алгебре также удобно описывается умножением матриц: это главная причина унифицирующей роли матричного языка и некоторой самостоятельности матричной алгебры внутри линейной алгебры. Перечислим некоторые из этих ситуаций. 6. Матрица композиции линейных отображений. Пусть P, N, M - три конечномерных линейных пространства,
Следовательно, (j, k)-й элемент матрицы Afg равен Согласно результатам пп. 3-5 множество линейных операторов -1-2-3-4-5-6-7-8-9-10-11-12-13-14-15- |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник



 - два линейных отображения. Выберем базисы
- два линейных отображения. Выберем базисы 

 и {em} в P, N, M соответственно и обозначим через Ag, Af, Afg матрицы g, f, fg в этих базисах. Мы утвержаем, что Afg = AfAg. В самом деле, пусть Af = (ajl), Ag = (bik). Имеем
и {em} в P, N, M соответственно и обозначим через Ag, Af, Afg матрицы g, f, fg в этих базисах. Мы утвержаем, что Afg = AfAg. В самом деле, пусть Af = (ajl), Ag = (bik). Имеем







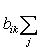





 , т. е. Afg = AfAg.
, т. е. Afg = AfAg.
 после выбора базиса в L можно отождествить с множеством квадратных матриц Mn(
после выбора базиса в L можно отождествить с множеством квадратных матриц Mn(
 , отвечают обратимые матрицы: если f
, отвечают обратимые матрицы: если f  f - 1 = idL, то AfA -1 = En, так что A -1 = Af-1. Напомним, что матрица A обратима, или невырождена тогда и только тогда, когда
f - 1 = idL, то AfA -1 = En, так что A -1 = Af-1. Напомним, что матрица A обратима, или невырождена тогда и только тогда, когда 
 .
.