Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Структура линейного отображения / 1 2 3 4 5 6 7 8 9 10
Значит,
т. к. 13. Примеры. а) Пусть f = idL, dim L = n. Тогда характеристический многочлен f равен (t - 1)n, а минимальный многочлен равен t - 1, так что они не совпадают при n > 1. б) Пусть f представлен жордановой клеткой Далее,
где единицы стоят на k-й диагонали выше главной; Jr(0)k = 0 при
при |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник


 для любого вектора
для любого вектора 
 . Следовательно,
. Следовательно,





 переводит в нуль любой вектор из L1. Это завершает доказательство.
переводит в нуль любой вектор из L1. Это завершает доказательство.
 . Характеристический многочлен оператора f равен
. Характеристический многочлен оператора f равен 
 . Чтобы вычислить минимальный многочлен, заметим, что
. Чтобы вычислить минимальный многочлен, заметим, что 


 .
.







 . С другой стороны,
. С другой стороны,



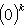


 , а поскольку минимальный многочлен - делитель характеристического, это доказывает, что они совпадают.
, а поскольку минимальный многочлен - делитель характеристического, это доказывает, что они совпадают.