Линейные пространства и линейные отображения / Структура линейного отображения / 1 2 3 4 5 6 7 8 9 10
Если поле   алгебраически замкнуто, то согласно теореме п. 6 любой линейный оператор алгебраически замкнуто, то согласно теореме п. 6 любой линейный оператор   имеет собственное подпространство. Однако он все равно может оказаться недиагонализируемым, т. к. сумма всех собственных подпространств может оказаться меньше L, тогда как у диагонализируемого оператора она всегда равна L. Прежде чем переходить к общему случаю, разберемся с комплексными имеет собственное подпространство. Однако он все равно может оказаться недиагонализируемым, т. к. сумма всех собственных подпространств может оказаться меньше L, тогда как у диагонализируемого оператора она всегда равна L. Прежде чем переходить к общему случаю, разберемся с комплексными   -матрицами. -матрицами.
8. Пример. Пусть L - двумерное комплексное пространство с базисом, оператор   представлен в этом базисе матрицей представлен в этом базисе матрицей   . Характеристический многочлен для f равен t2 - (a + d)t + (ad - bc), его корни . Характеристический многочлен для f равен t2 - (a + d)t + (ad - bc), его корни 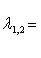 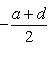 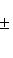 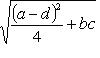 . Рассмотрим отдельно следующие случаи: . Рассмотрим отдельно следующие случаи:
а) 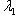 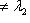 . Пусть e1 - собственный вектор для . Пусть e1 - собственный вектор для 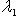 , e2 - для , e2 - для 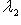 . Они линейно независимы, потому что если ae1 + be2 = 0, то . Они линейно независимы, потому что если ae1 + be2 = 0, то
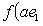 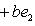 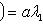 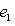 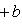 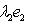 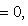
откуда 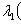 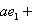 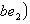 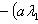 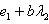 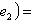 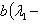 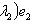 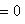 , т. е. b = 0 и аналогично a = 0. Следовательно, в базисе {e1, e2} матрица f диагональна. , т. е. b = 0 и аналогично a = 0. Следовательно, в базисе {e1, e2} матрица f диагональна.
б) 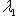 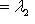 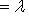 . Здесь оператор f диагонализируем, только если он умножает на . Здесь оператор f диагонализируем, только если он умножает на  все векторы из L: это значит, что все векторы из L: это значит, что 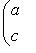 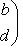 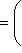 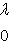  , т. е. , т. е. 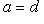 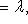 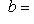 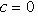 . Если же эти условия не выполнены, а выполнено только более слабое условие (a - d)2 + 4bc = 0, гарантирующее, что . Если же эти условия не выполнены, а выполнено только более слабое условие (a - d)2 + 4bc = 0, гарантирующее, что 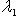 = = 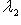 , то у оператора f может быть, с точностью до пропорциональности, только один собственный вектор и f заведомо не диагонализируем. , то у оператора f может быть, с точностью до пропорциональности, только один собственный вектор и f заведомо не диагонализируем.
-1-2-3-4-5-6-7-8-9-10-
|

 имеет собственное подпространство. Однако он все равно может оказаться недиагонализируемым, т. к. сумма всех собственных подпространств может оказаться меньше L, тогда как у диагонализируемого оператора она всегда равна L. Прежде чем переходить к общему случаю, разберемся с комплексными
имеет собственное подпространство. Однако он все равно может оказаться недиагонализируемым, т. к. сумма всех собственных подпространств может оказаться меньше L, тогда как у диагонализируемого оператора она всегда равна L. Прежде чем переходить к общему случаю, разберемся с комплексными 
 -матрицами.
-матрицами.
 . Характеристический многочлен для f равен t2 - (a + d)t + (ad - bc), его корни
. Характеристический многочлен для f равен t2 - (a + d)t + (ad - bc), его корни 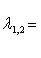
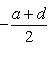
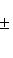
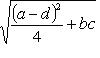 . Рассмотрим отдельно следующие случаи:
. Рассмотрим отдельно следующие случаи: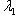
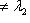 . Пусть e1 - собственный вектор для
. Пусть e1 - собственный вектор для 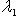 , e2 - для
, e2 - для 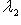 . Они линейно независимы, потому что если ae1 + be2 = 0, то
. Они линейно независимы, потому что если ae1 + be2 = 0, то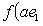
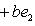
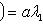
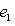
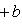
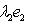
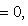
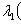
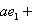
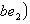
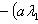
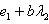
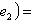
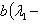
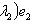
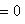 , т. е. b = 0 и аналогично a = 0. Следовательно, в базисе {e1, e2} матрица f диагональна.
, т. е. b = 0 и аналогично a = 0. Следовательно, в базисе {e1, e2} матрица f диагональна.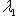
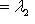
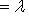 . Здесь оператор f диагонализируем, только если он умножает на
. Здесь оператор f диагонализируем, только если он умножает на  все векторы из L: это значит, что
все векторы из L: это значит, что 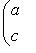
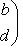
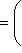
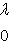
 , т. е.
, т. е. 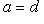
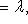
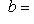
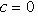 . Если же эти условия не выполнены, а выполнено только более слабое условие (a - d)2 + 4bc = 0, гарантирующее, что
. Если же эти условия не выполнены, а выполнено только более слабое условие (a - d)2 + 4bc = 0, гарантирующее, что