в) Рассмотрим многочлен M(t) со старшим коэффициентом единица, аннулирующий f и имеющий наименьшую возможную степень. Он называется минимальным многочленом оператора f. Очевидно, он определен однозначно: если M₁(t), M₂(t) - два таких многочлена, то M₁(t) - M₂(t) аннулирует f и имеет строго меньшую степень, так что M₁(t) - M₂(t) = 0.

г) Покажем, что любой многочлен, аннулирующий f, делится на минимальный многочлен f. Действительно, пусть Q(f) = 0. Разделим Q с остатком на M: Q(t) = X(t)M(t) + R(t), deg R(t) < deg M(t). Тогда R(f) = Q(f) - X(f)M(f) = 0, так что R = 0.

12. Теорема Гамильтона - Кэли. Характеристический многочлен P(t) оператора f аннулирует этот оператор.

Доказательство. Мы будем пользоваться этой теоремой и докажем ее только для случая алгебраически замкнутого поля , хотя она верна и без этого ограничения.

Проведем индукцию по dim L. Если L одномерно, то f есть умножение на скаляр и P(f) = 0.

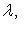
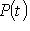
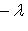
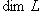
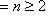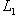
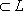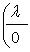
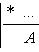
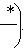
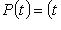
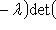
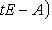Пусть и теорема доказана для пространств размерности n - 1. Выберем собственное значение оператора f и одномерное собственное подпространство , отвечающее . Пусть {e₁} - базис L₁; дополним его до базиса {e₁, ..., e_n} пространства L. Матрица оператора f в этом базисе имеет вид

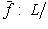
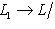
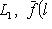
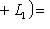
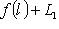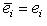
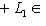
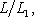
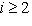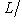
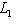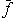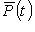
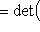
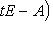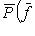
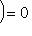Поэтому . Оператор f определяет линейное отображение . Векторы , образуют базис , и матрица оператора в этом базисе равна A. Поэтому есть характеристический многочлен оператора , и по индуктивному предположению .

-1-2-3-4-5-6-7-8-9-10-