Справочник формул
| Подробный список разделов |
| Линейные пространства и линейные отображения |
| Геометрия пространств со скалярным произведением |
| Аффинная и проективная геометрия |
| Полилинейная алгебра |
основные математические формулы
|
Линейные пространства и линейные отображения / Структура линейного отображения / 1 2 3 4 5 6 7 8 9 10
10. Пример. Пусть
(первое слагаемое отсутствует при i = 0). Следовательно,
Таким образом, функции 11. Кроме уже рассмотренных геометрических соображений для нужд следующего параграфа нам понадобятся алгебраические сведения о полиномиальных функциях от оператора. Пусть а) Для любого многочлена б) Будем говорить, что многочлен Q(t) аннулирует оператор f, если Q(f) = 0. Ненулевые многочлены, аннулирующие f, существуют всегда, если L конечномерно. В самом деле, если dim L = n, то |
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р
с
т
у
ф
х
ц
ч
ш
щ
э
ю
я
Линейная алгебра и геометрия
математические формулы, он-лайн справочник
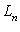
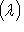 - линейное пространство комплексных функций вида
- линейное пространство комплексных функций вида 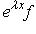
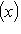 , где
, где 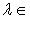
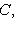
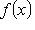 пробегает многочлены степени
пробегает многочлены степени 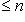
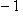 . Поскольку
. Поскольку 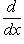
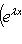
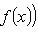
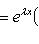
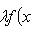
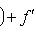
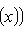 , дифференцирование
, дифференцирование 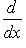 является линейным оператором на этом пространстве. Положим
является линейным оператором на этом пространстве. Положим 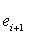
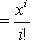
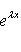 (напомним, что 0! = 1), i = 0, ..., n - 1. Очевидно,
(напомним, что 0! = 1), i = 0, ..., n - 1. Очевидно,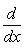
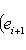
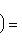
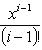
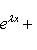
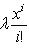
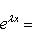
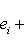
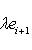
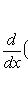
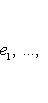
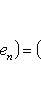
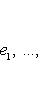
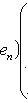
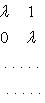
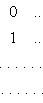

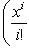
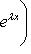 образуют жорданов базис для оператора
образуют жорданов базис для оператора 
 - фиксированный оператор.
- фиксированный оператор.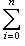
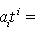
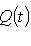 с коэффициентами из поля
с коэффициентами из поля 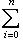
 имеет смысл в кольце
имеет смысл в кольце 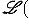
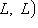 эндоморфизмов пространства L; мы будем обозначать его Q(f).
эндоморфизмов пространства L; мы будем обозначать его Q(f).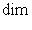

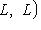
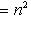 и операторы
и операторы 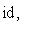
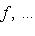
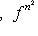 линейно зависимы над
линейно зависимы над 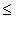
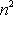 . На самом деле теорема Гамильтона - Кэли, которая будет доказана далее, устанавливает существование аннулирующего многочлена степени n.
. На самом деле теорема Гамильтона - Кэли, которая будет доказана далее, устанавливает существование аннулирующего многочлена степени n.